A volume failure
2024-09-24
Before we get into the failure, let me start with a picture.
On the left is a volumetric flask. The red arrow points at its “full” line. On the right is a graduated cylinder, also with a red arrow pointing at its full line. Volume markings on both are greyed out.
I would like you to guess, if I fill them both up to their respective full lines, which one holds more. Make two guesses: one under the assumption that this is not a trick question, and one under the assumption that it is.
Answer later.
Background
If you add 10 mL1 of water to 10 mL of water, you will end up with 20 mL of water.
But if you add 10 mL of water to, say, 10 mL of glycerol, and shake it up pretty well to mix them, you will end up with something that’s a little less than 20 mL of fluid2.
Fluid volumes are not additive if different fluids are involved.
That’s why volumetric flasks are a thing:

Because when you make a solution, the first thing you need to decide is what the final volume is going to be. And then you can use a recipe like this to figure out how much of each thing to put in:
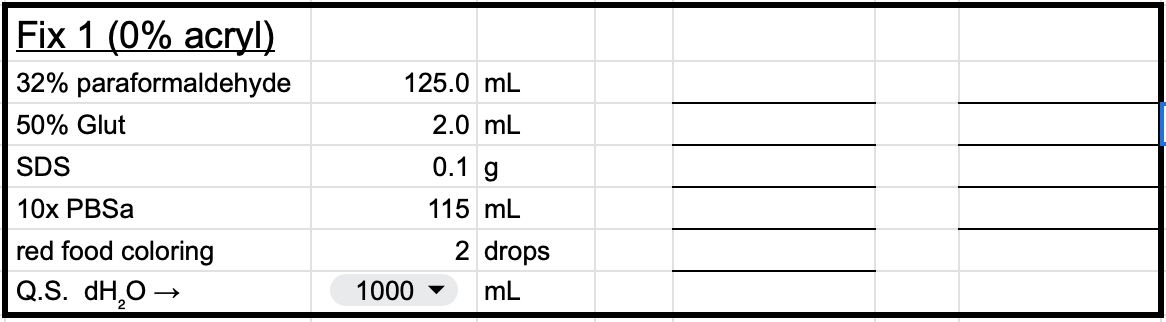
For example, if you want your final solution to be 4% formaldehyde, you take the final volume, 1000 mL, multiply by the destination (4%), divide by the source (32%), and end up knowing you need to pour 125 mL from your paraformaldehyde bottle into your volumetric flask. And so on with the other ingredients.
At the end, that final step there, you “Q.S.”—quantity sufficient3—with distilled water4 (dH2O) up to the final volume, which means that after you’ve added everything else into your volumetric flask, you pour in water just until it reaches that line on the neck.
Important for this story: at no point in time do you bother adding volumes together, nor do you try to guess ahead of time how much water you will need to reach the final total, since that doesn’t work.
Today’s failure
I wanted to make a solution that was 80% glycerol and 4% formaldehyde, in buffer. No problem. I worked out the recipe:
I didn’t mentally add the volumes together, because that’s not a thing you do with recipes. If I had, the problem would have been obvious. Sure, adding different fluids will add up to less than their total…but not by that much.
So when I tried to add 80 mL of glycerol, I hit the full line before it had all poured in. Nevermind even getting to the water step. (I slightly recommend muting the following video, since the main sound throughout is the roar of the fume hood).
After a few minutes of letting the gloopy glycerol slide back down to the bottom of the cylinder, it became clear that I had ended up with a 72% glycerol solution:
Oops.5
mL = milliliter. Something I did not fully realize before I started this job: 1 mL = 1 cc, where a “cc” is a cubic centimeter. When they say “10 ccs, stat” on medical shows, that’s just the same volume measurement as mL.
If I’d known ahead of time how I was going to structure this post, I would probably have tried it, and taken pictures. But I didn’t, and I’m writing this from home, so oh well.
A term my boss may or may not be the first to apply to this particular scenario.
Which we alternately write as “dH2O”, “d.i. water”, “DI”, and so on, because we can’t seem to settle on just one abbreviation for the most-used substance in the lab.
I might try re-making it using 10xPBS instead of 5xPBA. That would halve the buffer from 20mL to 10mL, which might or might not be enough. I don’t have a more concentrated version of paraformaldehyde, so that’s the best I could do. I might just use the 72% though.
The answer to the original question is in the video: they both are 100 mL. They sure don’t look the same, though, do they?




